Contact
제품, 인재 채용, 투자 관련 또는 기타 문의사항이 있으신 경우 편하신 방법으로 연락주시기 바랍니다
문의하기

summary
Score-based generative modeling (NCSN v1)은 데이터 분포를 이해하기 위한 접근법으로, Kingma가 2014년에 활용한 Variational Inference의 개념에서 출발하여 꼼꼼히 수식적으로 NCSN v1의 나머지 부분과 실험 및 저자들의 insight를 따라가 본다.
Denoising Score Matching
위 식 \((5) \)를 다시 써보자.
\(\begin{align}\frac{1}{2}\mathbb{E}\bigg[-2\big\langle s_{\theta}(x),\nabla_x\log p_{data}(x)\big\rangle\bigg] &=-\int p_{data}(x)\bigg\langle s_{\theta}(x),\frac{\partial \log p_{data}(x)}{\partial x}\bigg\rangle dx\nonumber\\ &=-\int p_{data}(x)\bigg\langle s_{\theta}(x),\frac{\frac{\partial p_{data}(x)}{\partial x}}{p_{data}(x)}\bigg\rangle dx\nonumber\\ &=-\int\bigg\langle s_{\theta}(x),\frac{\partial p_{data}(x)}{\partial x}\bigg\rangle dx\nonumber\\ &=-\int\bigg\langle s_{\theta}(x),\frac{\partial}{\partial x}\int p_{data}(\widetilde{x})p_{data}(x|\widetilde{x})d\widetilde{x}\bigg\rangle dx\\ &=-\int\bigg\langle s_{\theta}(x),\int p_{data}(\widetilde{x})\frac{\partial p_{data}(x|\widetilde{x})}{\partial x}d\widetilde{x}\bigg\rangle dx\nonumber\\ &=-\int\int p_{data}(\widetilde{x})\frac{p_{data}(x|\widetilde{x})}{p_{data}(x|\widetilde{x})}\bigg\langle s_{\theta}(x), \frac{\partial p_{data}(x|\widetilde{x})}{\partial x}\bigg\rangle d\widetilde{x}dx\nonumber\\ &=-\int\int p_{data}(\widetilde{x})p_{data}(x|\widetilde{x})\bigg\langle s_{\theta}(x), \frac{1}{p_{data}(x|\widetilde{x})}\frac{\partial p_{data}(x|\widetilde{x})}{\partial x}\bigg\rangle d\widetilde{x}dx\nonumber\\ &=-\int\int p_{data}(\widetilde{x})p_{data}(x|\widetilde{x})\bigg\langle s_{\theta}(x),\frac{\partial}{\partial x}\log p_{data}(x|\widetilde{x})\bigg\rangle d\widetilde{x}dx\nonumber\\ &=-\mathbb{E}_{p_{data}(x,\widetilde{x})}\bigg[\bigg\langle s_{\theta}(x),\frac{\partial}{\partial x}\log p_{data}(x|\widetilde{x})\bigg\rangle\bigg]\end{align} \)
(9)
(10)
이 식 \((10)\)을 다시 식 \((4)\)에 넣으면
\(\begin{align}\mathcal{L}_{\theta}&=\frac{1}{2}\mathbb{E}_{x\sim p_{data}(x)}\bigg[\big\|s_{\theta}(x)\|^2-2\big\langle s_{\theta}(x),\nabla_x\log p_{data}(x)\big\rangle\bigg]\nonumber\\ &=\mathbb{E}_{x\sim p_{data}(x)}\bigg[\frac{1}{2}\|s_{\theta}(x)\|^2\bigg] - \mathbb{E}_{p_{data}(x,\widetilde{x})}\bigg[\bigg\langle s_{\theta}(x),\frac{\partial\log p_{data}(x|\widetilde{x})}{\partial x}\bigg\rangle\bigg]\end{align}\)
(11)
가 된다. 식 전개가 좀 복잡했지만 따라왔을 것이라 믿는다. 이 식의 의미는 무엇일까?
바로 식 \( (8)\)에 있는 \(\text{tr}(\nabla_xs_{\theta}(x))\) 를 우회하기 위함이다. 즉, 사전에 지정된 noise를 첨가하여 perturbation을 걸어준 데이터의 분포 \(\log p_{data}(x|\widetilde{x})\) 의 score를 추정하여 원래 목적했던 score matching을 수행하는 것이다.
Sliced Score Matching
Sliced Score Matching에서는 식 \((2)\)를 사영(projection)을 통해 접근한다. 먼저,
\(L(\theta;p_v):=\frac{1}{2}\mathbb{E}_{p_v}\mathbb{E}_{p_{data}}\bigg[(v^Ts_{\theta}(x)-v^T\nabla_x\log p_{data}(x))^2\bigg]\)
을 정의하자. 이 때 두 가지 가정을 한다. 첫 번째는 \(p_{data} \)는 미분 가능하고 그 도함수가 연속이라는 것이고, 두 번째는 projection vector \(v\) 에 대해서 \(\mathbb{E}_{p_v}[\|v\|^2]<\infty \) 이며 \(\mathbb{E}_{p_v}[vv^T]\succ0\) 이라는 것(positive definite matrix)이다.
\(\begin{align}L(\theta;p_v)&=\frac{1}{2}\mathbb{E}_{p_v}\mathbb{E}_{p_{data}}\bigg[(v^Ts_{\theta}(x)-v^T\nabla_x\log p_{data}(x))^2\bigg]\nonumber\\ &=\mathbb{E}_{p_v}\mathbb{E}_{p_{data}}\bigg[v^T\nabla_xs_{\theta}(x)v + \frac{1}{2}(v^T\nabla_x\log p_{data}(x))^2\bigg] + C\end{align}\)
(12)
이 때 \(C\)는 \(\theta\)에만 의존하는 constant이다. 이를 보이자. 먼저
\(\begin{align}L(\theta;p_v)&=\frac{1}{2}\mathbb{E}_{p_v}\mathbb{E}_{p_{data}}\bigg[(v^Ts_{\theta}(x)-v^T\nabla_x\log p_{data}(x))^2\bigg]\nonumber\\ &=\frac{1}{2}\mathbb{E}_{p_v}\mathbb{E}_{p_{data}}\bigg[(v^Ts_{\theta}(x))^2 + (v^T\nabla_x\log p_{data}(x))^2 - 2(v^Ts_{\theta}(x))(v^T\nabla_x\log p_{data}(x))\bigg]\nonumber\\ &=\mathbb{E}_{p_v}\mathbb{E}_{p_{data}}\bigg[-(v^Ts_{\theta}(x))(v^T\nabla_x\log p_{data}(x)) + \frac{1}{2}(v^Ts_{\theta}(x))2\bigg]+C \end{align}\)
(13)
로 전재하고 나면 우리가 보여야 할 것은
\(\begin{equation}-\mathbb{E}_{p_v}\mathbb{E}_{p_{data}}\bigg[(v^Ts_{\theta}(x))(v^T\nabla_x\log p_{data}(x))\bigg] = \mathbb{E}_{p_v}\mathbb{E}_{p_{data}}\bigg[v^T\nabla_xs_{\theta}(x)v\bigg]\end{equation}\)
(14)
이라는 주장이다. 위 식을 정직하게 전개해보면
\(\begin{align}-\mathbb{E}_{p_v}\mathbb{E}_{p_{data}}\bigg[(v^Ts_{\theta}(x))(v^T\nabla_x\log p_{data}(x))\bigg]&=-\mathbb{E}_{p_v}\int p_{data}(x)(v^Ts_{\theta}(x))(v^T\nabla_x\log p_{data}(x))dx\nonumber\\ &=-\mathbb{E}_{p_v}\int (v^Ts_{\theta}(x))(v^T\nabla_xp_{data}(x))dx\\&=-\mathbb{E}_{p_v}\sum_{i=1}^N\int(v^Ts_{\theta}(x))v_i\frac{\partial p_{data}(x)}{\partial x_i}dx\end{align}\)
(15)
(16)
가 된다. 이제 각 \(i\)번째 변수에 대해서 부분적분을 수행해 보면, \((16)\)식은
\(\begin{align}-\mathbb{E}_{p_v}\bigg[\sum_{i=1}^N\int(v^Ts_{\theta}(x))v_i\frac{\partial p_{data}(x)}{\partial x_i}dx\bigg]&=-\mathbb{E}_{p_v}\bigg[\sum_{i=1}^N\bigg(\bigg[(v^Ts_{\theta}(x))v_ip_{data}(x)\bigg]^{\infty}_{-\infty}-\int\big(v^T\frac{\partial s_{\theta}(x)}{\partial x_i}\big)v_ip_{data}(x)dx\bigg)\nonumber\\ &=\mathbb{E}_{p_v}\bigg[\sum_{i=1}^N\int(v^T\frac{\partial s_{\theta}(x)}{\partial x_i})v_ip_{data}(x)dx\bigg]\nonumber\\ &=\mathbb{E}_{p_v}\bigg[\sum_{i=1}^N\int(v^T\nabla_xs_{\theta}(x))v_ip_{data}(x)dx\bigg]\nonumber\\ &=\mathbb{E}_{p_v}\int p_{data}(x)v^T\nabla_xs_{\theta}(x)vdx\nonumber\\ &=\mathbb{E}_{p_v}\mathbb{E}_{p_{data}}\big[v^T\nabla_xs_{\theta}(x)v\big] \end{align}\)
(17)
를 얻을 수 있다. 따라서 식 \((2)\)는
\(\begin{equation}\mathbb{E}_{p_v}\mathbb{E}_{p_{data}}\bigg[v^Ts_{\theta}(x)v + \frac{1}{2}\|s_{\theta}(x)\|^2\bigg]\end{equation}\)
(18)
를 최적화하는 것과 동치이다.
Sampling with Langevin dynamics
Langevin dynamcis에 따르면 다음과 같은 식을 통해 inference를 진행하게 된다:
\(\tilde{x}_t = \tilde{x}_{t-1} + \frac{\epsilon}{2}\nabla_x\log p(\tilde{x}_{t-1})+\sqrt{\epsilon}z_t\)
이 때 \( z_t\sim\mathcal{N}(0,I)\)의 noise로 생각한다. 이 과정에서 필요한 것은 score function만임을 주의하자.
Challenges of score-based generative modeling
The manifold hypothesis
Manifold hypothesis라는 가설은 데이터가 고차원 공간에 있지만, 실제로 데이터를 설명하는 변수(혹은 차원)은 몇 개 안된다는 주장이다. 이를 수학적으로 이야기하면 data는 high-dimension 속에 embedding되어 있는 low-dimensional manifold에 얹어져 있다는 말로 생각할 수 있다. 그런데 문제는, manifold는 continuous한 것인데 비하여 data points는 discrete하다. 따라서 저자들은 support를 넓히기(무한대로 만들기) 위해 데이터에 noise perturbation을 아주 살짝 걸어준다. 이는 \(\mathcal{N}(0, 0.0001)\)정도로 사람은 전혀 눈치채지 못할 수준이다. 그렇게 하면, score function이 학습이 가능해진다!
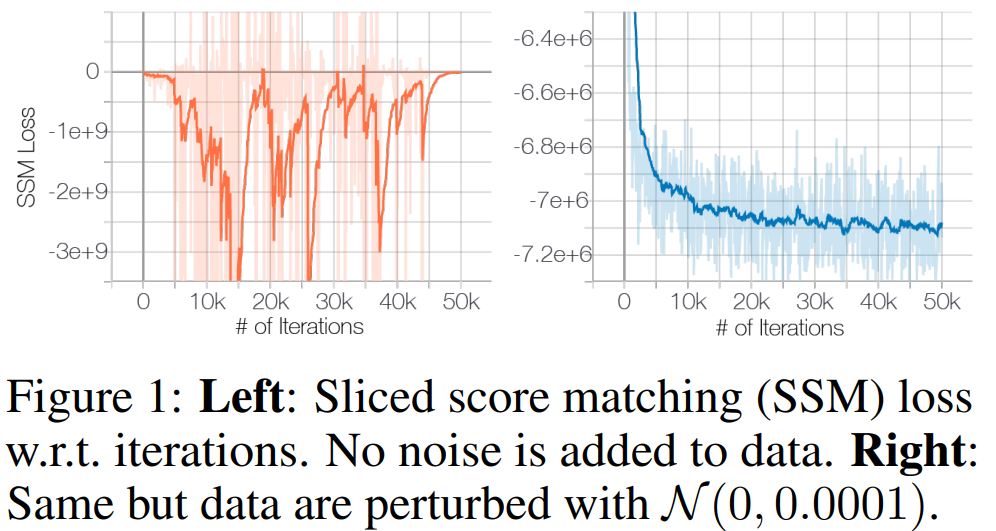
Inaccurate score estimation with score matching
앞서 살펴보았듯 score matching의 objective는 \(\mathbb{E}_{p_{data}}[\|s_{\theta}(x)-\nabla_x\log p_{data}(x)\|^2]\) 이다. 실제 데이터에서는 하지만 data의 sparsity 때문에 \(p_{data}(\mathcal{R})\approx0\) 이 되는 \(\mathcal{R}\subset\mathbb{R}^D\)가 가 존재한다. 이 경우에 거의 대부분에서는 \(\{x_i\}_{i=1}^N\cap\mathcal{R}\approx\emptyset\)일 것이고 score matching은 적절한 score function을 예측하지 못할 것이다. 이를 toy example에 대해 실험한 것이 다음 그림이다:
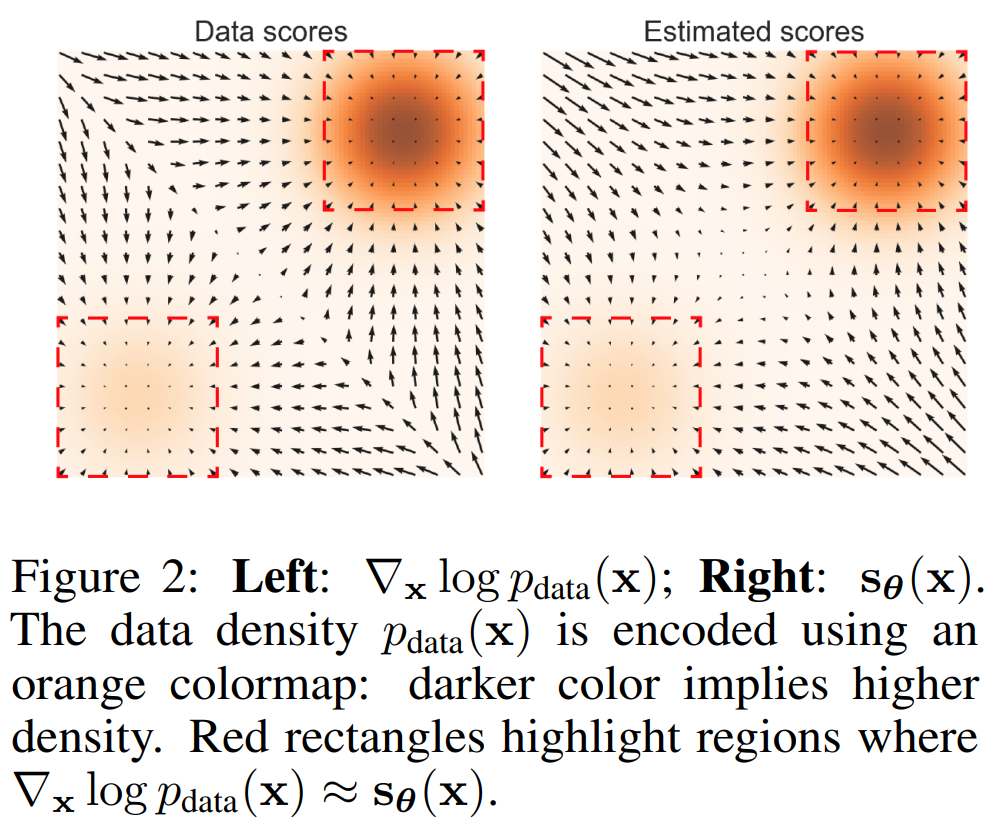
위 그림에서 붉은 사각형 바깥에 있는 대각선 방향으로 자세히 살펴보면 화살표들의 방향이 다르게 위치함을 알 수 있다.
Slow mixing of Langevin dynamics
두 분포가 섞인 mixuture distribution \(p_{data}(x)=\pi p_1(x) + (1-\pi)p_2(x)\)를 생각하자. 이 때 \(p_1\)과 \(p_2\)는 서로 다른 support를 가진다. 단순 계산을 해보면, \(p_1\)의 support에서, \(\nabla_x\log p_{data}(x)=\nabla_x\log p_1(x) \)가 될 것이고 \(p_2\)의 support에서는 \(\nabla_x\log p_{data}(x)=\nabla_x\log p_2(x)\) 가 될 것이다. 각 경우에 대해서 \(\pi\)항이 사라짐을 알 수 있다. 즉, score는 두 분포의 계수인 \(\pi\)를 알려주지 않는다.
이에 대한 그림이 다음이다:
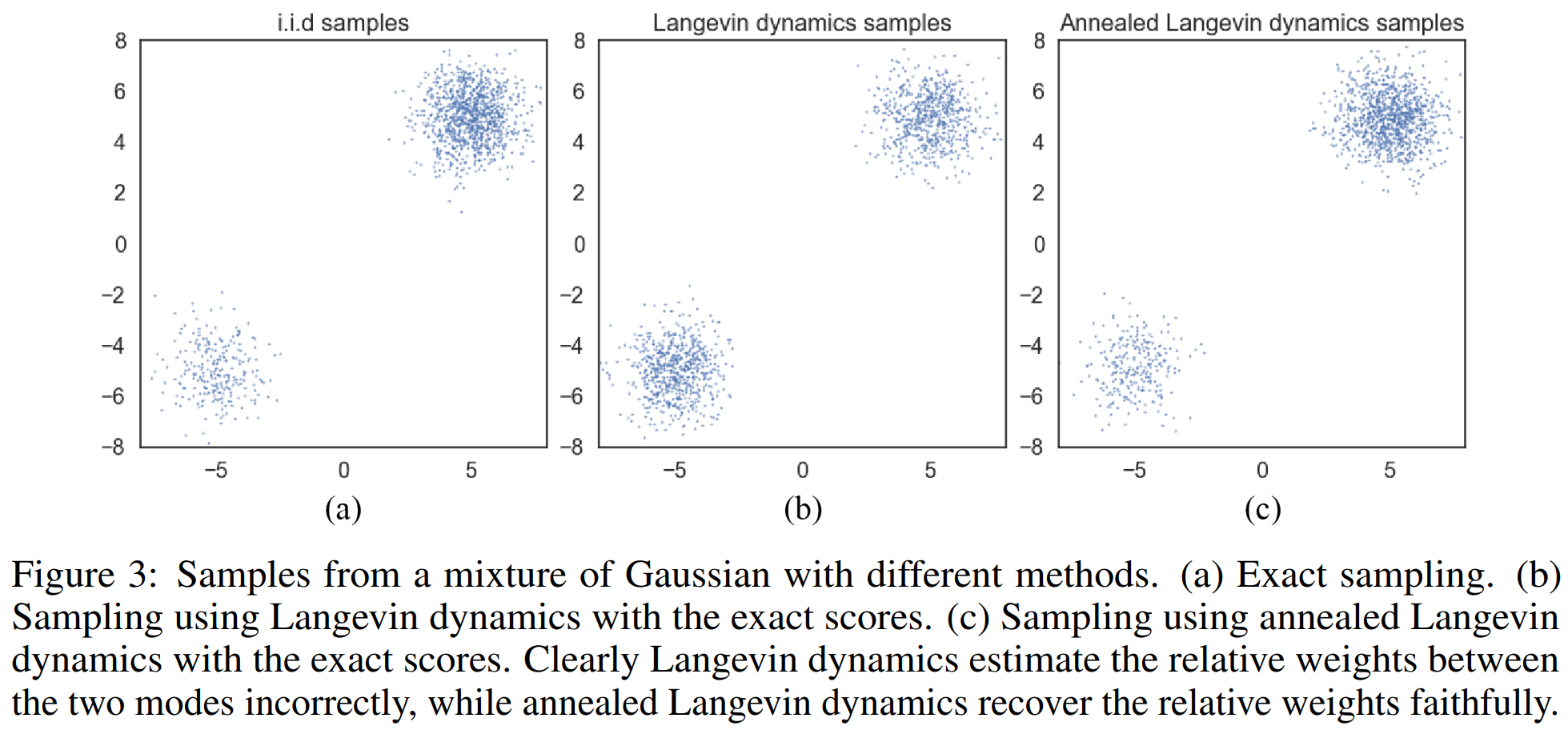
정확히 Langevin dynamics 그 자체를 사용한 (b)에서는 데이터의 sampling 밀도 차이가 원래 비율이었던 (a)와 다르게 된다. 하지만 저자들이 주장하는 annealed Langevin dynamics를 사용하면 썩 괜찮게 sample들이 비율을 맞춰 추출되게 된다.
Noise Conditional Score Networks: learning and inference
Noise Conditional Score Networks
\(\{\sigma_i\}_{i=1}^L\)을 \(\frac{\sigma_1}{\sigma_2}=\cdots=\frac{\sigma_{L-1}}{\sigma_L}>1\)을 만족하는 양의 등비급수라고 하자. \(q_{\sigma}(x):=\int p_{data}(t)\mathcal{N}(x|t,\sigma^2I)dt\)를 data에 perturbation을 건 것이라고 하자. 그리고 \(\sigma_1\)을 크게, \(\sigma_L\) 을 작게 잡아서 score를 잘 예측하고자 한다. 이렇게 학습한 network인 \(s_{\theta}(x,\sigma)\)를 noise conditional score network (NCSN)이라고 한다.
Learning NCSNs via score matching
Sliced score matching과 denoising score matching 모두를 통해서 NCSN을 학습시킬 수 있지만 본 논문에서 저자들은 denoising 방법론이 더 빠르고 noise-perturbated data distribution에 맞는다고 생각하여 이 방법론을 썼다. 이를 학습하기 위해 noise distribution을 \(q_{\sigma}(\widetilde{x}|x)=\mathcal{N}(\widetilde{x}|x,\sigma^2I)\)로 정의하였다. 따라서 \(\nabla_{\widetilde{x}}\log q_{\sigma}(\widetilde{x}|x)=-(\widetilde{x}-x)/\sigma^2\)이 된다. \( \sigma\)를 정해놓고 나면, denoising score matching의 target은
\(l(\theta;\sigma):=\frac{1}{2}\mathbb{E}_{p_{data}(x)}\mathbb{E}_{\widetilde{x}\sim\mathcal{N}(x,\sigma^2I)}\bigg[\bigg\|s_{\theta}(\widetilde{x},\sigma)+\frac{\widetilde{x}-x}{\sigma^2}\bigg\|^2\bigg]\)
이 된다. 따라서 이를 \(\sigma_i\)에 대해 모두 더한
\(\mathcal{L}(\theta;\sigma):=\frac{1}{L}\sum_{i=1}^L\lambda(\sigma_i)l(\theta;\sigma_i)\)
가 최종 loss function이 된다. 테크니컬 한 측면에서 저자들은 실험적으로 \(\|s_{\theta}(x,\sigma)\|\propto1/\sigma\)임을 관찰했고 따라서 \(\lambda(\sigma)=\sigma^2\)으로 두기로 했다고 한다. 그러면 당연히
\(\lambda(\sigma)l(\theta;\sigma)=\sigma^2l(\theta;\sigma)=\frac{1}{2}\mathbb{E}\bigg[\bigg\|\sigma s_{\theta}(\widetilde{x},\sigma)+\frac{\widetilde{x}-x}{\sigma}\bigg\|^2\bigg] \)
이 된다. 이렇게 scale을 맞춰주는 작업을 하였다.
NCSN inference via annealed Langevin dynamics
아래 알고리즘이 annealed Langevin dynamics이다.
Results
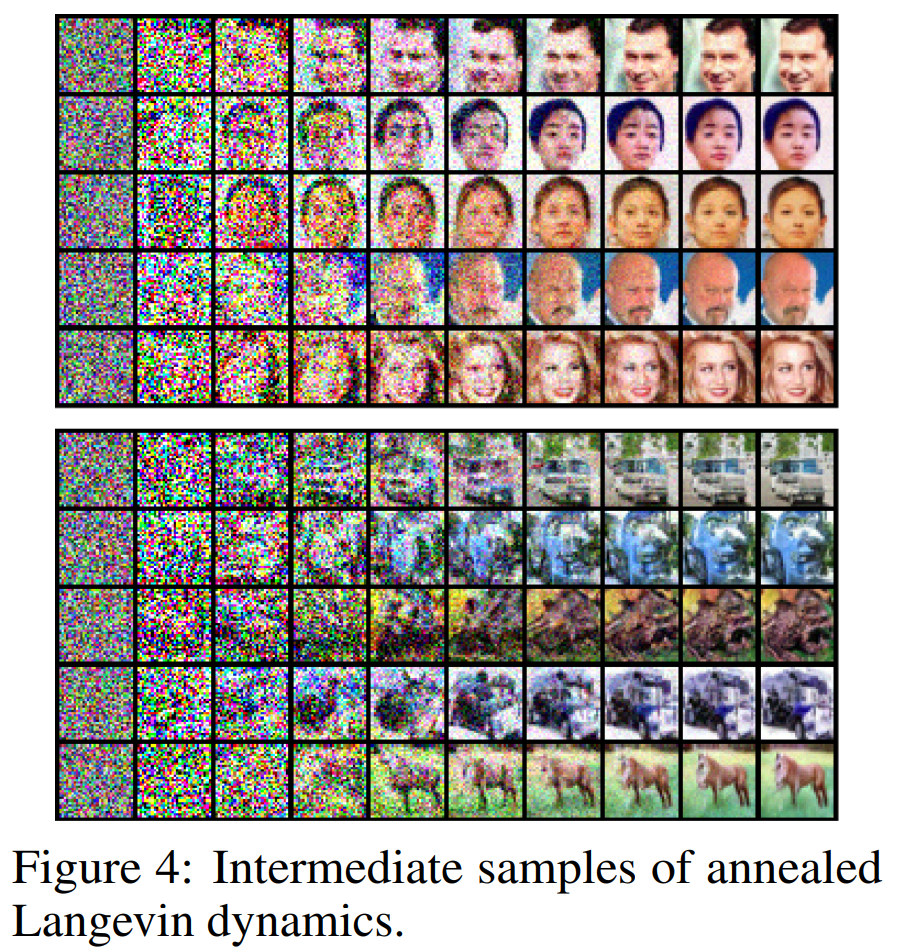

실험 결과는 상당히 인상깊지만, 고화질의 이미지를 제공하고 있지는 않고 실제로 이것이 문제가 된다. 이를 해결하기 위해 저자들은 후속 논문을 작성했고, 다음 글에서 살펴보도록 한다.
문의하기